
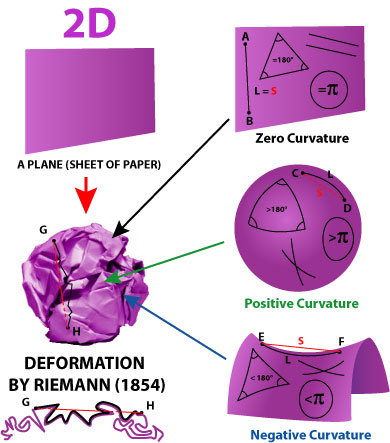
The strength of the new techniques used here allowed us to prove also a homology version of Theorem A, which is given in Theorem B. Call a metric space proper if the closure of every metric ball is compact (i.e. $$$$Īnd being harder to construct, have a different nature and genesis: the former classes – given in – come from the existence of exotic spheres, while the latter classes – given here – arise from the non-triviality and structure of certain homotopy groups of the space of pseudo-isotopies of the circle Abstract: We prove that the harmonic measures on the spheres of a pinched Hadamard manifold admit uniform upper and lower bounds. alpha + beta + gamma < pi The angle at the vertices follows the relation alpha + beta + gamma pi - A/R2 Zero Curvature. Annales de lInstitut Fourier (Cellule MathDoc/CEDRAM) - Vol. Consider a negatively curved space (a saddle shown in the following image), the sum of interior angles of the triangle is less than 180 o, i.e. This result follows from Theorem A, which proves that the quotient map Harmonic measures on negatively curved manifolds. (In a flat Universe the angles would add up to 180 degrees exactly. Scalar-tensor (ST) gravity theories provide an appropriate theoretical framework for the variation of Newton's fundamental constant, conveyed by the dynamics of a scalar-field non-minimally coupled to the. Our main result states that, for certain k-spheres This means that if large triangles could be ‘drawn’ in space, their internal angles would add up to less than 180 degrees. This contributes a basic framework to build up a parametrised pseudo-newtonian formalism adequate to test ST negatively curved space-times. We look at some rigidity properties related to isometric embeddings into Minkowski space. For a space X there is a forgetful map Fīetween bundle theories over X, which assigns to a bundle with negatively curved fibers over X its subjacent smooth bundle. This short note is a mostly expository article examining negatively curved three-manifolds. In the first part of the paper we introduce the theory of bundles with negatively curved fibers.
Teichmüller Spaces and Negatively Curved Fiber Bundles Teichmüller Spaces and Negatively Curved Fiber Bundles


 0 kommentar(er)
0 kommentar(er)
